本帖最后由 周伯通 于 2022-1-14 23:07 编辑
为啥春节抢红包总不是手气最佳?看完微信抢红包算法你就明白了。
2022-01-13 14:46
PK创意闹新春,我正在参加「春节创意投稿大赛」,详情请看:春节创意投稿大赛”
前言春节必不可少的活动就是抢红包啦,从以前的纸质红包到现在互联网红包(以微信红包为首),今天我们就来分析一下抢红包的算法,其中有一些是微信红包的算法,看完你就知道手气最佳是如何产生的啦!
算法一:剩余金额随机法算法一是不推荐使用的,算法一全称叫剩余金额随机法,听名字就知道这个方法是将剩余的金额进行随机分配,我们先来看代码。 // 分配红包的算法private static void testPocket(BigDecimal amount, BigDecimal min, BigDecimal num) {BigDecimal remain = amount.subtract(min.multiply(num));final Random random = new Random();final BigDecimal hundred = new BigDecimal("100");BigDecimal sum = BigDecimal.ZERO;BigDecimal redpeck ;for (int i = 0; i < num.intValue(); i++) { final int nextInt = random.nextInt(100); if (i == num.intValue() - 1) { redpeck = remain; } else { redpeck = new BigDecimal(nextInt).multiply(remain).divide(hundred, 2, RoundingMode.FLOOR); } if (remain.compareTo(redpeck) > 0) { remain = remain.subtract(redpeck); } else { remain = BigDecimal.ZERO; } sum = sum.add(min.add(redpeck)); System.out.println("第" + (i + 1) + "个人抢到红包金额为:" + min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP));}System.out.println("红包总额:" + sum.setScale(2, BigDecimal.ROUND_HALF_UP));}// 测试代码public static void main(String[] args) { BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP); testPocket2(amount,min,num);}复制代码
我们可以看到,这个方法是有很明显的缺陷的,就是一开始领到红包的人获取的金额可能是最大的,后面领取的金额就逐渐变小了,因为他是从剩余额金额进行随机的。很显然微信是肯定不会使用这种方法作为红包瓜分算法,不然每次一有红包,马上领取就有可能获取手气最佳,但是明显不是。
算法二:整体随机法整体金额随机法的公式:红包总额 * 随机数/随机数总和,这个方法的核心是使用一个随机数作为红包瓜分的标准,这个随机数是通过Random类随机产生的。他的随机性就比较大了,看起来好像是和我们平时抢红包差不多,但是微信红包也不是采用这种方法,因为这种的随机性太大了,不是很公平。 private static void testPocket2(BigDecimal amount,BigDecimal min ,BigDecimal num){ final Random random = new Random(); final int[] rand = new int[num.intValue()]; BigDecimal sum1 = BigDecimal.ZERO; BigDecimal redpeck ; int sum = 0; for (int i = 0; i < num.intValue(); i++) { rand = random.nextInt(100); sum += rand; } final BigDecimal bigDecimal = new BigDecimal(sum); BigDecimal remain = amount.subtract(min.multiply(num)); for (int i = 0; i < rand.length; i++) { if(i == num.intValue() -1){ redpeck = remain; }else{ redpeck = remain.multiply(new BigDecimal(rand)).divide(bigDecimal,2,RoundingMode.FLOOR); } if(remain.compareTo(redpeck) > 0){ remain = remain.subtract(redpeck); }else{ remain = BigDecimal.ZERO; } sum1= sum1.add(min.add(redpeck)).setScale(2, BigDecimal.ROUND_HALF_UP); System.out.println("第"+(i+1)+"个人抢到红包金额为:"+min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP)); } System.out.println("红包总额:"+sum1);}// 测试代码public static void main(String[] args) { BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP); testPocket2(amount,min,num);}复制代码
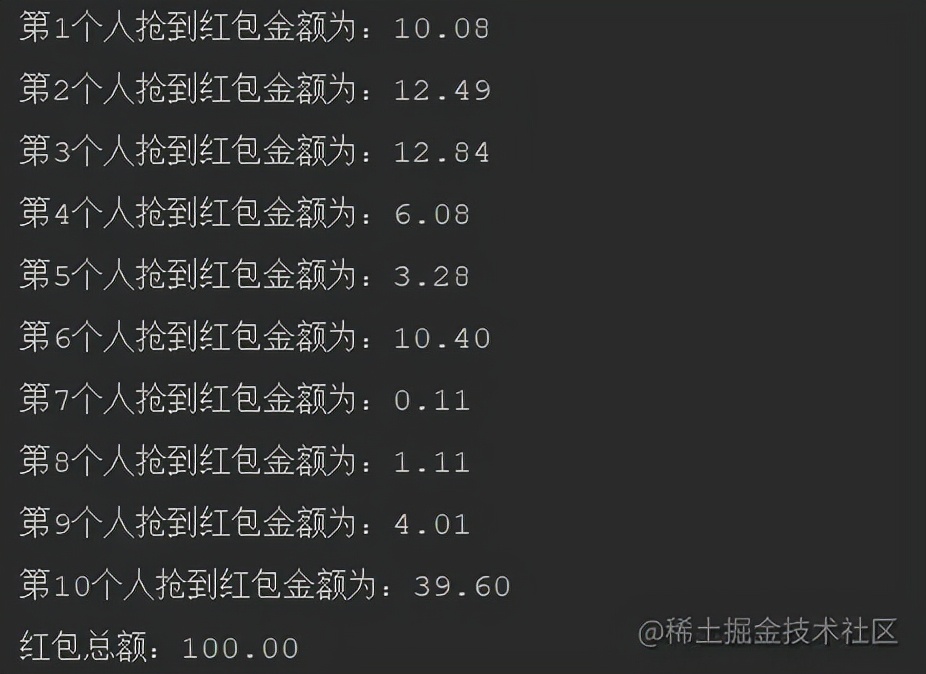
他的随机性可谓是很高,也不是最佳选择。
算法三:割线法割线法指的是把红包总金额想象成一条很长的线段,而每个人抢到的金额,则是这条主线段所拆分出的若干子线段,当所有切割点确定以后,子线段的长度也随之确定。这样每个人来抢红包的时候,只需要顺次领取与子线段长度等价的红包金额即可。
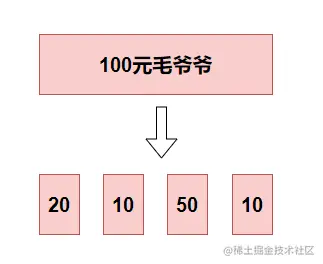
private static void testPocket3(BigDecimal amount, BigDecimal min, BigDecimal num) { final Random random = new Random(); final int[] rand = new int[num.intValue()]; BigDecimal sum1 = BigDecimal.ZERO; BigDecimal redpeck; int sum = 0; for (int i = 0; i < num.intValue(); i++) { rand = random.nextInt(100); sum += rand; } final BigDecimal bigDecimal = new BigDecimal(sum); BigDecimal remain = amount.subtract(min.multiply(num)); for (int i = 0; i < rand.length; i++) { if (i == num.intValue() - 1) { redpeck = remain; } else { redpeck = remain.multiply(new BigDecimal(rand)) .divide(bigDecimal, 2, RoundingMode.FLOOR); } if (remain.compareTo(redpeck) > 0) { remain = remain.subtract(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP); } else { remain = BigDecimal.ZERO; } sum1 = sum1.add(min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP)); System.out.println("第" + (i + 1) + "个人抢到红包金额为:" + min.add(redpeck)); } System.out.println("红包总额:" + sum1);}// 测试代码public static void main(String[] args) { BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP); BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP); testPocket2(amount,min,num);}复制代码
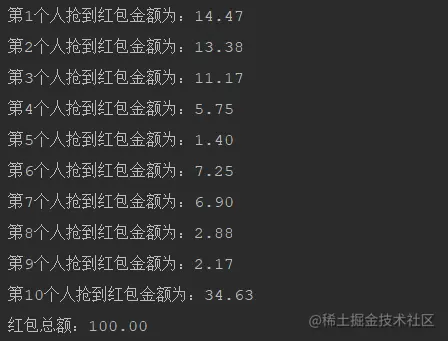
他的随机性也比较大,但是他最致命的是性能,因为他需要进行切割这个步骤。
算法四:二倍均值法算法四就是微信红包目前所采用的的算法(大致思路,代码模拟),二倍均值计算公式:2 * 剩余金额/剩余红包数。 BigDecimal remain = amount.subtract(min.multiply(num)); final Random random = new Random(); final BigDecimal hundred = new BigDecimal("100"); final BigDecimal two = new BigDecimal("2"); BigDecimal sum = BigDecimal.ZERO; BigDecimal redpeck; for (int i = 0; i < num.intValue(); i++) { final int nextInt = random.nextInt(100); if(i == num.intValue() -1){ redpeck = remain; }else{ redpeck = new BigDecimal(nextInt).multiply(remain.multiply(two).divide(num.subtract(new BigDecimal(i)),2,RoundingMode.CEILING)).divide(hundred,2, RoundingMode.FLOOR); } if(remain.compareTo(redpeck) > 0){ remain = remain.subtract(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP); }else{ remain = BigDecimal.ZERO; } sum = sum.add(min.add(redpeck)).setScale(2, BigDecimal.ROUND_HALF_UP); System.out.println("第"+(i+1)+"个人抢到红包金额为:"+min.add(redpeck)); } System.out.println("红包总额:" +
sum);}复制代码
他还是比较好的保证了每个红包金额大致相等,不会出现极端情况。
|